The object of the present chapter is to show that it is more consistent with the attributes of the Deity to look upon miracles not as deviations from the laws assigned by the Almighty for the government of matter and of mind; but as the exact fulfilment of much more extensive laws than those we suppose to exist. In fact, if we were endued with acuter senses and higher reasoning faculties, they are the very points we should seek to observe, as the tests of any hypothesis we had been led to frame concerning the nature of [92/93] those laws. Even with our present imperfect faculties we frequently arrive at the highest confirmation of our views of the laws of nature, by tracing their action under singular circumstances.
The mode by which I propose to arrive at these conclusions is, by again appealing to the judgment which each individual will himself form, when examining that piece of mere human mechanism, to which the argument so frequently compels me to advert. If he agrees with me, that the second of the two views presented to him exhibits a higher degree of knowledge, and a higher exertion of power, than the first, he must inevitably conclude, that the view here suggested of the nature of miracles, assigns a far higher degree of knowledge and power to the Deity.
Let the reader suppose himself placed before the calculating engine, and let him again observe and ascertain, by lengthened [93/94] induction, the nature of the law it is computing. Let him imagine that he has seen the changes wrought on its face during the lapse of thousands of years, and that, without one solitary exception, he has found the engine register the series of square numbers. Suppose, now, the maker of that machine to say to the observer, "I will, by moving a certain mechanism, which is invisible to you, cause the " engine to make one cube number instead " of a square, and then to revert to its former "course of square numbers;" the observer would be inclined to attribute to him a degree of power but little superior to that which was necessary to form the original engine.
But, let the same observer, after the same lapse of time — the same amount of uninterrupted experience of the uniformity of the law of square numbers, hear the maker of the engine say to him— "The next number which shall appear on those wheels, and which you expect to find a square number, shall [94/95] not be so. When the machine was originally ordered to make these calculations, I impressed on it a law, which should coincide with that of square numbers in every case, except the one which is now about to appear; after which no future exception can " ever occur, but the unvarying law of the squares shall be pursued until the machine itself perishes from decay."
Undoubtedly the observer would ascribe a greater degree of power to the artist who had thus willed that event which he foretells at the distance of ages before its arrival.
If the contriver of the engine then explain to him, that, by the very structure of it, he has power to order any number of such apparent deviations from its laws to occur at any future periods, however remote, and that each of these may be of a different kind; and, if he also inform him, that he gave it that structure in order to meet events, which he foresaw must [95/96] happen at those respective periods, there can be no doubt that the observer would ascribe to the inventor far higher knowledge than if, when those events severally occurred, he were to intervene, and temporarily to alter the calculations of the machine.
If, besides this, the contriver were so far to explain the structure of the engine that the observer could himself, by some simple process, such as the mere moving of a bolt, call into action those apparent deviations whenever certain combinations were presented to his eye; if he were thus to impart a power of predicting such excepted cases, dependent on the will, though in other respects beyond the limits of the observer's power and knowledge, —such a structure would be admitted as evidence of a still more skilful contrivance.
The engine which, in a former chapter, I introduced to the reader, possesses these powers. It may be set, so as to obey any [96/97] given law; and, at any periods, however remote, to make one or more seeming exceptions to that law. It is, however, to be observed, that the apparent law which the spectator arrived at, by an almost unlimited induction, is not the full expression of the law by which the machine acts; and that the excepted case is as absolutely and irresistibly the necessary consequence of its primitive adjustment, as is any individual calculation amongst the countless multitude which it may previously have produced.
When the construction of that engine was first attempted, I did not seek to give to it the power of making calculations so far beyond the reach of mathematical analysis as these appear to be: nor can I now foresee a probable period at which they may become practically available to human purposes. I had determined to invest the invention with a degree of generality which should include a wide range of mathematical power; and I was [97/98] well aware that the mechanical generalisations I had organised contained within them much more than I had leisure to study, and some things which will probably remain unproductive to a far distant day.
Amongst those combinations which I was afterwards induced to examine, I observed the powers I have now recorded; and the reflections they produced in my own mind, impelled me to pursue them for a time. If the reader agrees with me in opinion, that these speculations lead to a more exalted view of the great Author of the universe than any we have hitherto possessed, he must also have arrived at the conclusion, that the study of the most abstract branch of practical mechanics, combined with that of the most abstruse portions of mathematical science, has no tendency to incapacitate the human mind from the perception of the evidences of natural religion; and that even those very sources themselves may furnish arguments which open views of the grandeur of creation [98/99] perhaps more extensive than any which the sciences of observation or of physics have yet supplied.
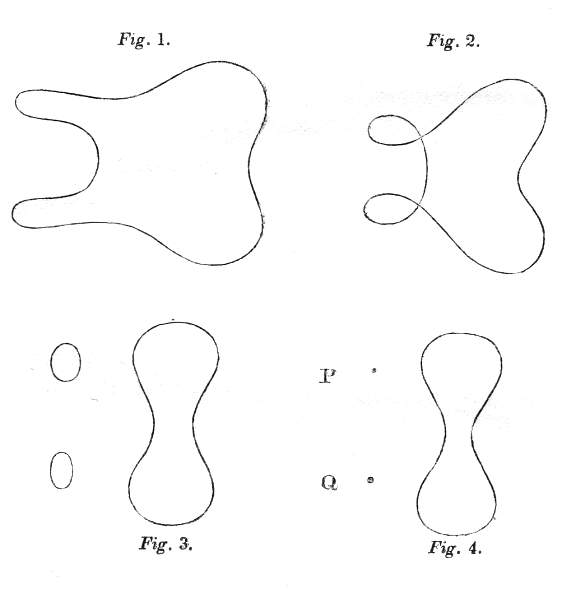
It may not, perhaps, be without its use to suggest another illustration derived from the same quarter respecting the nature of miracles. It is known that mathematical laws are sometimes expressed by curves. The figure 1 (p. 101) represents a re-entering curve of four dimensions, whose law of formation is given in the note.2 A slight change in the nature of the constants makes it assume the form of fig. 2, which is still a continuous curve; but a further change of the constants causes it to have two ovals, quite disconnected from the larger portion; and, as the constants again alter, these ovals are reduced to points. [99/100] In all four cases, every point in each branch of the curve obeys the same general law. The points, P and Q, though strictly invisible to the eye, are yet detected by mathematical analysis, and fulfil as precisely the original equation as any of the infinite number of other points, which constitute the rest of the curve. These points might be situated on the curve itself, and they are well known to mathematicians. It is to these singular points, which really fulfil the law of the curve, but which present to those who judge of them only by the organ of sight an apparent discontinuity, that I wish to call the attention, as offering an illustration of the doctrine here explained respecting miracles.
It has been remarked, in the beginning of the present chapter, that it is to the singular points—to those points of such infinitely rare occurrence in a curve—that we frequently have recourse, as the test of our theories, for explaining the phenomena of nature. [100/101]
[102/103] The existence of conical refraction in certain crystals, under peculiar circumstances, was predicted by Sir W. Hamilton; and, from an analytical investigation into the nature of the curve surface, which represents the form of the luminiferous wave within the crystal, he ascertained that it had four conoidal cusps, at each of which there were, consequently, an infinite number of tangent planes. The course of the refracted ray being determined by the tangent plane to the wave surface, it followed that a single ray within the crystal, transmitted in the direction of the line joining two opposite cusps, corresponded to an infinite number of refracted rays without, constituting a refracted cone.
A second case of conical refraction, predicted by Sir William Hamilton, depended on another mathematical fact—namely, that the wave surface is touched in an infinite number of points, constituting a small circle of contact, by a single plane parallel to one of the circular sections of the surface of elasticity. [103/104]
Professor Lloyd undertook to make the very delicate experiments required for this most interesting investigation. Of its great importance he was fully aware, for he remarks—
"Here, then, are two singular and unexpected consequences of the undulatory theory, " not only unsupported by any facts hitherto observed, but even opposed to all the analogies derived from experience. If confirmed "by experiment, they would furnish new and "almost convincing proofs of that theory; and, if disproved, on the other hand, it is evident that the theory must be abandoned or modified.3
On examining the first of these cases, experimentally, the fact of conical refraction was fully established. But a new result now presented itself: the rays of light thus conically [104/105] refracted were found to be polarized; and it was observed, that the angle between the planes of polarization of any two rays of the cone was half the angle between the planes, containing the rays themselves, and the axis."
This new law, thus approximately obtained by experiment, led the observer back to the theory; and, on a further examination, he detected in that theory the very law he had just discovered by observation.
The second case of conical refraction required experiments of a still more delicate nature. They were, however, made, and succeeded equally. The conically refracted ray was found to be polarised, according to the law which, in this instance, analysis had predicted; and, to complete the triumph of this union of theory and experiment, the measures in both cases, when made under proper circumstances, accorded with the theoretical conclusions, [105/106] within such limits as might be fairly attributed to the unavoidable errors of observation.
It is worthy of remark, that, at first, two facts presented themselves, which seemed to be at variance with the theory. In the first place, the emergent rays formed a solid cone, instead of a conical surface; and, in the second place, the calculated angle, subtended by the sides of the cone, was only one half the observed angle. Both the facts were shown to depend upon the size of the aperture through which the light was admitted, and to arise from the rays which were inclined at small angles to the single theoretical direction. When the aperture was diminished, so as to be very small, (the case calculated by Sir William Hamilton,) then the cone of light became truly a conical surface, and the observed angle was the same as the calculated one.4
12 December 2008